Robert Hummel

ROBERT HUMMEL

Network Optimization

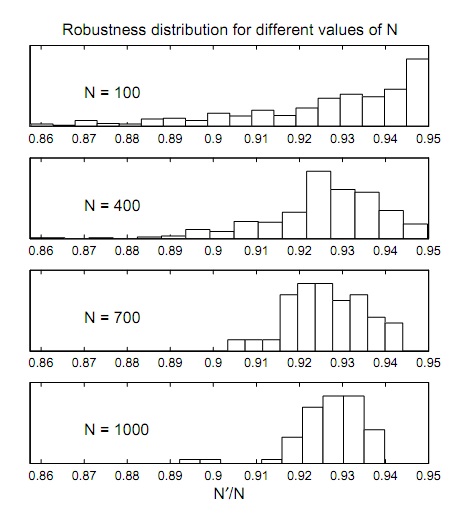
We address the early design of complex, large-scale systems by viewing them as random networks and optimizing structure over their generative parameters. In this approach, we do not seek speciﬁc topologies, but rather classes of near-optimal networks which correspond to desirable statistical behavior, while also allowing ﬂexibility to accommodate unmodeled constraints.

Functionally, we perform the optimization of generative parameters on small networks (e.g., one hundred nodes) and use the results to design large networks (e.g., one thousand or more nodes). This approach is a computationally feasible forward design path for large-scale systems.

A numerical example is given in which a network’s degree distribution is optimized for combined robustness and cost in a cascading failure scenario; the work has direct application to distributed communication systems.

For more information:

Hummel, R., J. Taylor, and F. Hover, "Numerical Optimization of Generative Network Parameters," ASME International Mechanical Engineering Congress and Exposition (IMECE), Vancouver, November 2010. (Full Text, PDF)

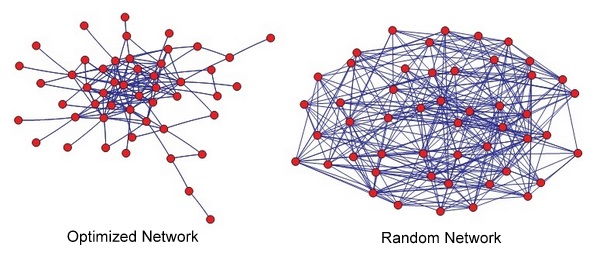The networks shown here have the same number of connections, yet the optimized network is much more robust to failure than the random network.

Optimized and random networks

We optimize a network using a particle swarm optimization on the degree distribution, which is the probability distribution of the number of edges on each node. The optimization is performed on small networks (N=100), and the result is used to build larger networks. The concept of averageability is displayed here – the performance of the networks converges in probability as the network size increases.

These results give us confidence that a large network that is generated with the degree distribution optimized on small networks will perform as expected.

Network Averageability